- Aturan Segitiga
Luas
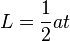 |
atau | 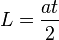 |
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang alas segitiga |
| 2. | 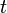 |
Tinggi segitiga |
 |
atau |  |
atau |
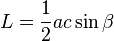 |
atau |  |
atau |
 |
atau |  |
|
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang sisi a, terletak diseberang sudut A |
| 2. | 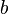 |
Panjang sisi b, terletak diseberang sudut B |
| 3. |  |
Panjang sisi c, terletak diseberang sudut C |
| 4. |  |
Besar sudut yang terletak di sudut A |
| 5. |  |
Besar sudut yang terletak di sudut B |
| 6. | 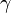 |
Besar sudut yang terletak di sudut C |
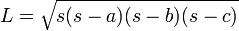
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang sisi a, terletak diseberang sudut A |
| 2. | 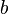 |
Panjang sisi b, terletak diseberang sudut B |
| 3. |  |
Panjang sisi c, terletak diseberang sudut C |
| 4. |  |
Setengah keliling segitiga  |
Keliling
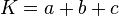
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang sisi a, terletak diseberang sudut A |
| 2. | 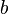 |
Panjang sisi b, terletak diseberang sudut B |
| 3. |  |
Panjang sisi c, terletak diseberang sudut C |
Teorema Pythagoras
215px 140px
 atau
atau atau
atau
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang dari sisi terpanjang/hipotenusa, selalu terletak diseberang sudut siku-sikunya. |
| 2. | 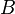 |
Panjang sisi lainnya |
| 3. | 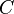 |
Panjang sisi lainnya |
- Teorema Pythagoras hanya berlaku pada segitiga siku-siku
Aturan Sinus

| Parameter | ||
|---|---|---|
| 1. |  |
Panjang sisi a, terletak diseberang sudut A |
| 2. | 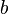 |
Panjang sisi b, terletak diseberang sudut B |
| 3. |  |
Panjang sisi c, terletak diseberang sudut C |
| 4. |  |
Besar sudut yang terletak di sudut A |
| 5. |  |
Besar sudut yang terletak di sudut B |
| 6. | 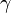 |
Besar sudut yang terletak di sudut C |
| 7. |  |
Jari-jari lingkaran luar segitiga |
Aturan Cosinus
 atau
atau atau
atau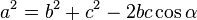
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang sisi a, terletak diseberang sudut A |
| 2. | 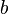 |
Panjang sisi b, terletak diseberang sudut B |
| 3. |  |
Panjang sisi c, terletak diseberang sudut C |
| 4. |  |
Besar sudut yang terletak di sudut A |
| 5. |  |
Besar sudut yang terletak di sudut B |
| 6. | 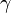 |
Besar sudut yang terletak di sudut C |
Aturan Tangen
![\frac{a-b}{a+b} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}](https://upload.wikimedia.org/math/a/2/a/a2a5f5d5d533d41d23bd4fa92b009ce7.png)
| Parameter | ||
|---|---|---|
| 1. |  |
Panjang sisi a, terletak diseberang sudut A |
| 2. | 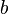 |
Panjang sisi b, terletak diseberang sudut B |
| 3. |  |
Panjang sisi c, terletak diseberang sudut C |
| 4. |  |
Besar sudut yang terletak di sudut A |
| 5. |  |
Besar sudut yang terletak di sudut B |
| 6. | 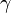 |
Besar sudut yang terletak di sudut C |



Materinya banyak mel .buat anak sma cukup
BalasHapusCukup ar ,tapi masih banyak yang harus dilengkapi di bangun ruang
BalasHapus